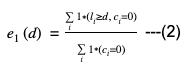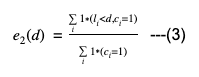事業者は、顧客が取引関係をいつ終わらせるのか、つまり「チャーン」という離脱行為がいつなされるのかを知る必要があります。サブスクリプションビジネスモデルでは、顧客は契約を能動的に解約することで取引関係から離脱します。したがって、企業はこのチャーンを確実に検知して記録することができます。しかし、明示的契約が存在しない場合、チャーンはむしろ受動的であり、検知することが困難です。顧客から直接何らかのフィードバックがなければ、企業は、その顧客が取引関係から一時的に離れているのか永久的に離れたのかを判断することができません。
これまでは、そういった契約のない取引関係のチャーンの検知は、ほとんど恣意的なものであり、科学的というよりも感覚的なものでした。
さまざまなアナリストが、あらゆる方法で、契約のないチャーンの難問に取り組んでいます。ある一般的なアプローチでは、顧客が十分に長い連続した期間にわたり取引を行わない場合に、その顧客が離脱したものと推定します。このアプローチの問題点は、それが根拠のない推測であることに加え、チャーンと判定するまでの期間の長さのしきい値を高くし過ぎることが多いという点です。これでは、事業者が相当長く待たなければチャーンの問題を識別できないことになります。『Prediction of Advertiser Churn for Google Adwords』では、著者は12か月後までチャーンを測定できないのです。そのように長期間待っていたのでは、チャーンを検知する意味は薄くなり、事業者が問題に対処する能力も下がります。チャーン判定期間を購入サイクル (顧客の購入から次の購入までの期間) の分布における特定のパーセンタイルとして推定する分析で、最適なパーセンタイル (90番目、95番目、99番目等) を選択することは困難です。
このブログでは、契約のないチャーンを定義するための、科学的なアプローチを紹介します。このアプローチでは、第一種過誤と第二種過誤を良定義の目的関数で最小化することにより、苦労して最適なパーセンタイルを選択する手間を回避できます。
理論
チャーン判定期間 (d) とは、これを超えると顧客との取引関係が終了したと考えられる、連続した沈黙 (取引のない) 期間の最小値です。企業は一般的に、顧客をアクティブ顧客とチャーン顧客とに分けます。顧客との取引関係が契約に依存しない場合、特定の d には、第一種過誤および第二種過誤があります。したがって、これらの過誤の目的関数を最小化する定義を選択しなければなりません。このアプローチでは、関数を過誤の加重平均であると規定します。
ここでの定義は次のようになります。
- e1(d) は、チャーン定義 d に関連して予想される第一種過誤です。この場合の第一種過誤とは、アクティブな顧客をチャーン顧客に分類することです。
- e2(d) は、チャーン定義 d に関連して予想される第二種過誤です。この場合の第二種過誤とは、チャーン顧客をアクティブ顧客に分類することです。
- w は、第二種過誤との関係でアナリストにより第一種過誤に設定された加重です。これは過誤の相対コストと解釈できます。
したがって、最適なチャーン定義 (d* で表す) で、F(d) が最小になります。この F(d) を d 曲線と呼びます。
誤差関数 e1(d) と e2(d) を計算するため、別の一連の表記法を紹介する必要があります。
- ci は、顧客 i の実際の離脱状況を表すもので、0はアクティブ、1はチャーンの状態を意味します。
- li は、顧客 i が取引を止めていた連続期間の数を表します。
上記の定義を使用すると、e1(d) と e2(d) は次のように導き出されます。
(2) と (3) から、e1(d) は誤ってチャーン顧客に分類されたアクティブ顧客の全体的な割合であることがわかります。同様に、e2(d) は誤ってアクティブ顧客に分類されたチャーン顧客の全体的な割合です。
理論の実装
ある時点 S から時点 T までの、すべての顧客取引に関する期間を記録したデータがあるとします。
最適なチャーン定義を判断するため、次の実験を行います。
- これを超えるとチャーン顧客だと判定できる最小の期間 D を定義します。これは、顧客の購入サイクルの分布 (連続する顧客取引日の期間の差) を調査し、十分高いパーセンタイルを選択することで可能です。ここでは、D を検証期間と呼ぶことにします。つまり、調査の対象が T-D より前に少なくとも1件の取引があった顧客に限定されなければ、顧客の本当の離脱状況 ci を算出することはできません。また、データ全体の長さ (T-S) は、d 曲線 F(d) の選択したチャーン定義の範囲を評価できる程度に、十分に長い必要があります。たとえば、範囲を {d:d<K+1) とする場合、T-S は K+D を超えていなければなりません。
- 自発的なチャーンのみに注目したい場合は、企業により非自発的に終了させられたその他すべての顧客を除去します。
- 各顧客 i について、時点 T における最終購入期間を確定します。
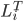
時点 T における休眠期間を算出します。
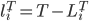
それから、本当の離脱状態を算出します。
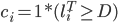
- 各顧客 i について、時点 T-D における最終購入期間を確定します。
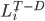時点 T-D における休眠期間を算出します。
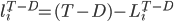
- チャーン定義の範囲 {d:dK}、つまり、F(d) を最小化したい範囲を選択します。
- 選択した範囲の各チャーン定義 d =0, 1, 2…K について、時点 T-D における各顧客の離脱状態を予測し、第一種過誤 e1(d) と第二種過誤 e2(d) を測定します。データから、 e1(d) と e2(d) は次のように計算できることがわかります。
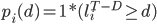
- 適切な加重 w を選択します。
- d=0, 1, 2, …K は、(1) を使用して F(d) となります。
- F(d) が最小になる d を、最適な d として選択します。
実世界に応用した結果
Indeed の契約のないサービスの1つとして有料のオプション (スポンサー求人) を識別し、パーセンタイル手法と d 曲線手法の両方を用いてチャーン判定期間を定めました。2016年9月 (S) から2019年9月 (T) までの月間取引データを使用しました。
ただし、公開するトレンドとインサイトは実際の調査結果に沿うものですが、Indeed のデータのセキュリティを保護するため、実際の結果を調整したものを示していますので留意してください。
パーセンタイル手法
このアプローチで、各顧客の購入サイクルを算出します。その結果、各顧客の購入サイクルの要約統計量 (平均値、中央値、および最大値) で各顧客を示すことができます。その後、別々の顧客に対して要約統計量の分布を作成します。
| 分位数 | 平均値 | 中央値 | 最大値 |
|---|---|---|---|
| 0 | 1 | 1 | 1 |
| 0.2 | 2 | 2 | 2 |
| 0.4 | 2 | 2 | 2 |
| 0.6 | 3.5 | 3 | 5 |
| 0.8 | 4.7 | 3 | 9 |
| 0.9 | 6.2 | 5 | 13 |
| 0.95 | 8 | 7 | 17 |
| 0.99 | 15 | 15 | 25 |
| 1 | 38 | 38 | 38 |
| すべて説明用の数値 | |||
これらの結果は、パーセンタイル手法に関連する分析のジレンマを例証するものです。分布は要約統計量の選択次第で変わります。一定の要約統計量を使用したとしても、どのパーセンタイル (90番目、95番目、または99番目) が最適なのかは明らかになりません。それとは別に、いずれのパーセンタイルを選択する場合でも、不必要に高いチャーン定義となります。たとえば、平均購入サイクルの分布の95パーセンタイルは8か月である一方、最大購入サイクルの分布では、なんと同じパーセンタイルが17か月にもなります。次のアプローチで、そのように定義が長くなるほど第一種過誤が減少する一方、第二種過誤が増大することを確認していきましょう。
d 曲線アプローチでは、第一種および第二種過誤の加重合計の最小値を用いてチャーン定義を選択することにより、これらの問題のすべてに対処します。
d 曲線アプローチ
このモデルを次のようにパラメーター化しました。
- w=0.5
- D=12
- S= 09-2016
- K=12
- T=09-2019
- T-D=09-2018
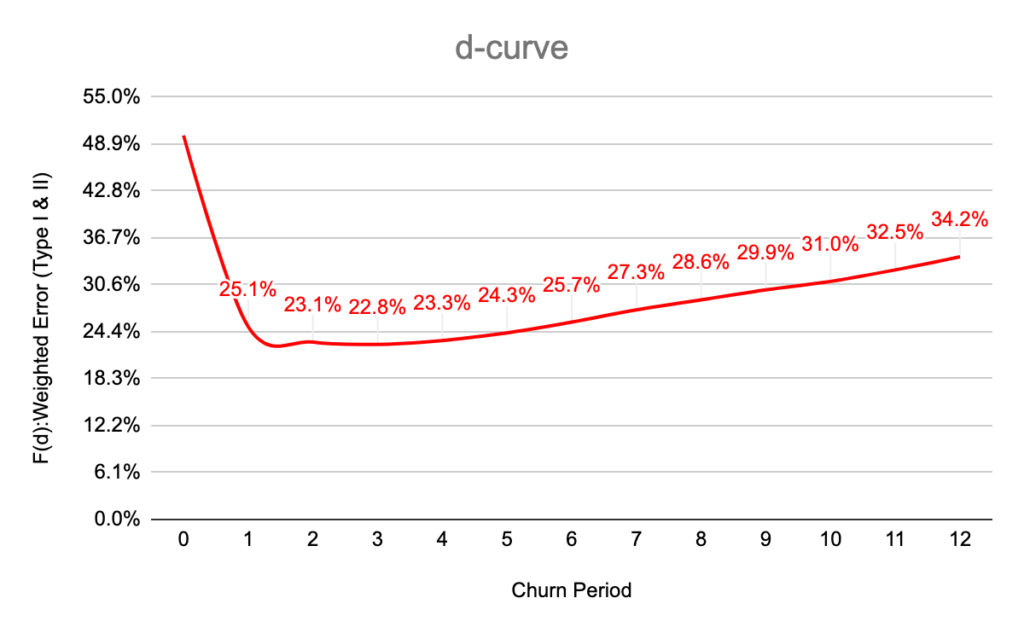
| チャーン判定期間 | 第一種過誤 (%) | 第二種過誤 (%) | 過誤の加重平均 (%) |
|---|---|---|---|
| 0 | 100.0 | 0.0 | 50.0 |
| 1 | 43.8 | 6.4 | 25.1 |
| 2 | 33.0 | 13.1 | 23.1 |
| 3 | 26.6 | 19.0 | 22.8 |
| 4 | 21.9 | 24.8 | 23.3 |
| 5 | 17.8 | 30.8 | 24.3 |
| 6 | 14.7 | 36.8 | 25.7 |
| 7 | 12.2 | 42.4 | 27.3 |
| 8 | 10.4 | 46.7 | 28.6 |
| 9 | 8.9 | 50.8 | 29.9 |
| 10 | 8.0 | 54.1 | 31.0 |
| 11 | 6.9 | 58.2 | 32.5 |
| 12 | 5.8 | 62.6 | 34.2 |
d 曲線を使用して、最適なチャーン定義として3か月を選択します。有意水準1%での仮説検定は、d=3の過誤は d=4の過誤に等しいとする帰無仮説を棄却します。
d 曲線のさらなる応用
しきい値を最適に選択できるよう、フレームワークを公式化しました。このアプローチは、契約のない取引関係のチャーン判定期間を定義するために適用できると同時に、代表的なものとしては分類におけるしきい値確率の決定など、その他の実世界での応用が数多くなされています。
謝辞
レビューと優れたフィードバックを寄せてくれた Trey Causey、Ehsan Fakharizadi、ならびに Yaoyi Chen に深く感謝します。この記事の内容に間違いがあった場合は、筆者である Gyasi Dapaa と Adesewa Adegoke にお知らせください。